EXP-RTL: Exponential Retaliation In Iterated Prisoner’s Dilemma Games
In the mathematical field of game theory, the iterated prisoner’s dilemma is a two-player, turn-based game in which participants can choose to cooperate with, or defect against, their opponents. Defections have higher payoffs, but carry the almost certain risk of retaliation by opposing players.
Over the years, hundreds of strategies have been developed for IPD, ranging from very simple (e.g. Tit-For-Tat, which simply mirrors its opponents last play), to highly complex, involving advanced math theories and drawing from psychology, biology, and evolutionary studies.
EXP-RTL (Exponential Retaliation) is my addition to the existing pool of strategies. EXP-RTL will cooperate if it makes the first the move of the game, and it will continue cooperating provided its opponent does the same.
If its opponent defects, EXP-RTL increments a _grudges variable by 1, computes the current value of _grudges raised to the second power, and adds the output to a _retaliations variable. It checks the value of _retaliations on every move and defects if it finds it greater than zero. _retaliations is decremented by 1 after each defection, and if it reaches zero, EXP_RTL will resume cooperating. _grudges is never decremented, so the amount of retaliation inflicted by EXP-RTL grows exponentionally with every defection it encounters.
I used the great Axelrod library, which has hundreds of IPD strategies bundled in a very accessible format, as well as some highly convenient tournament functions and evolutionary processes.
Below is an implentation of the strategy in the Python progromaming language:
import axelrod as axl
import matplotlib.pyplot as plt
import random
class EXP_RTL(axl.player.Player):
"""Player cooperates as long as Opponent does the same. If Opponent defects,
Player increments a _grudges variable by one, computes the current value of
_grudges raised to the second power and adds the output to a _retaliations
variable.
As long as _retaliations > 0, player will defect on every turn. After each
defection by Player, _retaliations is decremented by one, and Player won't
resume cooperating until _retaliations == 0.
If Opponent defects while Player is still retaliating, Player increments
_retaliations by the new value of grudges raised to the second power.
"""
name = "EXP-RTL"
classifier = {
"memory_depth": float("inf"),
"stochastic": False,
"makes_use_of": set(),
"long_run_time": False,
"inspects_source": False,
"manipulates_source": False,
"manipulates_state": False,}
def __init__(self):
super().__init__()
"""Inherits all the attributes and methods of the Player superclass and
initializes the variables that will be manipulated during gameplay.
"""
self._grudges = self._retaliations = 0
def strategy(self, opponent):
#Defines the strategy that will be used by the agent
C, D = axl.action.Action.C, axl.action.Action.D
if not opponent.history:
return C
if opponent.history[-1] == C:
if self._retaliations == 0:
return C
self._retaliations -= 1
return D
if opponent.history[-1] == D:
self._grudges += 1
self._retaliations += (self._grudges ** 2) - 1
return D
def tournament(self):
"""Runs a tournament between EXP_RTL and all non-longrunning
and non-cheating strategies in the Axelrod database. Strategies with very
high computational cost and/or try to "cheat", eg by modifying their own or
their opponents source code, have been excluded.
The results of the tournament are stored to file, along with a series of plots
that visualize the results.
"""
#Uncomment code below to run tournament with seed:
#axl.seed(0)
players = [self] + [
strategy() for strategy in axl.strategies
if strategy.classifier["long_run_time"] == False]
tournament = axl.Tournament(
players,
turns = 200,
repetitions = 5)
results = tournament.play()
# Write results to file
with open(
"results.txt",
"a",
encoding = "UTF-8") as resultsfile:
for player_rank in results.ranked_names:
resultsfile.write(f"{player_rank}\n")
# Write more comprehensive tournament summary to CSV file
results.write_summary("tournament_summary.csv")
# Create visual representations of the tournament results with plots
plot = axl.Plot(results)
"""All plots are saved to file, including boxplot,
winplot, payoff matrix, and more.
"""
plot.save_all_plots("tournament_visualization")
def moran_process(self):
"""Pits EXP_RTL and 19 strategies chosen at random in
the Moran process, a stochastic population process simulating natural selection.
Due to the method's high computational cost, only 20 strategies compete at a
time, but the random sampling ensures that different strategies are included
every time the method is called. with EXP-RTL being the only constant.
"""
players = [self] + [
strategy() for strategy in random.sample(
axl.strategies, k = 10) if strategy.classifier[
"long_run_time"] == False]
mp = axl.MoranProcess(
players = players,
turns = 200)
populations = mp.play()
# Write the sequence of populations to file
with open(
"population_sequence.txt",
"a",
encoding = "UTF-8") as sequences:
for sequence in populations:
sequences.write(f"{sequence}\n")
print("\n", f"Winning Strategy: {mp.winning_strategy_name}", "\n")
# Create a visual representation of the results
ax = mp.populations_plot()
plt.show()
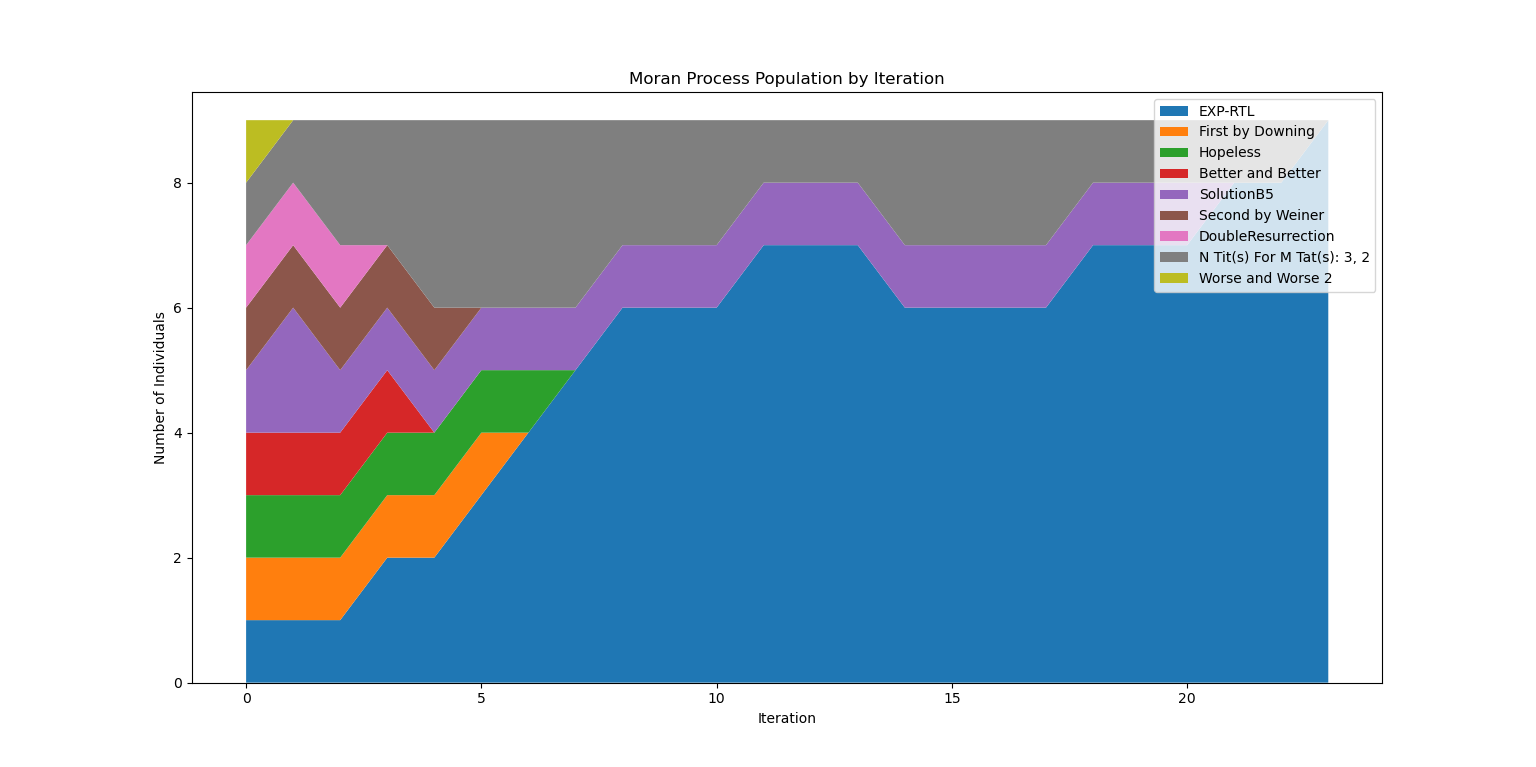
Below is a plot of EXP-RTL and nine other strategies competing in the Moran process, a technique that mimics natural selection. Note that this is without mutation.
Full code repo available on Github.
Related posts:
Square Neighborhood Algorithm: Balancing Exploration And Exploitation In Optimization
Interleaved Neighborhood Algorithm: Fully Exploratory Optimization
2020-04-02 00:01 +0000